Toàn cơ được thể hiện trong Lạc thư, một trong những thứ thuộc về thời tiền sử?

Tác giả: Cửu Số

[ChanhKien.org]

Ngước nhìn thiên văn, tinh di đẩu chuyển, chim bay thỏ chạy. Trong con mắt nhân loại, thiên địa thương khung chính là một bộ toàn cơ lớn. Bài viết này tiếp tục dùng phương thức toán thuật chữ số để giải Lạc thư, tìm hiểu cơ chế toàn cơ trong Lạc thư, cũng chính là toàn cơ thể hiện trong Lạc thư như thế nào.

4 9 2

3 5 7

8 1 6

Trước hết xin giới thiệu một quan điểm cơ bản về Lạc thư. Lạc thư người ta thường gọi là phương đồ (đồ hình vuông). Ví dụ cách sắp xếp của cửu cung số, ba hàng ba cột, rõ ràng là hình dạng của một hình vuông. Như vậy, Lạc thư cũng được gọi là phương đồ. Nhưng mà, cách nói này, chỉ được tính là một nửa, còn có một nửa nữa, Lạc thư cũng có thể gọi là viên đồ (đồ hình tròn). Cách giải thích của cổ nhân rất đơn giản, 9 5 1, 3 5 7, 4 5 6, 2 5 8, bốn nhóm số này đều có tổng là 15, rất giống với tính chất đường kính hình tròn. Như vậy, Lạc thư cũng được coi là một hình tròn với tâm là số 5, còn lại 8 số khác được phân bố đều quanh hình tròn.

Trong lịch sử, vấn đề Lạc thư bao gồm cả vuông lẫn tròn này, thì người nói rõ ràng nhất là Vạn Niên Thuần vào thời nhà Thanh. Vạn Niên Thuần là cử nhân vào thời Càn Long, từng làm chức huyện thái gia, có tác phẩm “Động Đình Hồ chí”. Trong các tác phẩm nho học của Vạn Niên Thuần, có một đồ hình Lạc thư ngoài tròn trong vuông. Tra khắp các sách vở của cổ nhân, tôi cho rằng đồ hình đó có mang theo thiên cơ sâu sắc. Cấu tạo của đồ hình Lạc thư ngoài tròn trong vuông như sau:

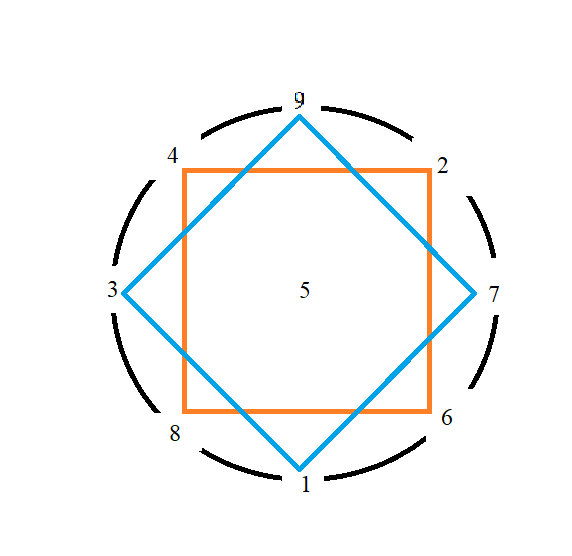
Vẽ một vòng tròn, đặt số 5 vào trung tâm, 8 số còn lại đặt ở trên đường tròn, xếp theo hình chữ 米 trong chữ Hán. 9 ở trên, 1 ở dưới, 3 bên trái, 7 bên phải, 4 ở góc trên bên trái, 6 ở góc dưới bên phải, 2 ở góc trên bên phải, 8 ở góc dưới bên trái.

Tiếp theo, 4 nối với 2, 2 nối 6, 6 nối 8, 8 nối 4. Đây là hình vuông số chẵn.

Sau đó, 9 nối 7, 7 nối 1, 1 nối 3, 3 nối 9. Đây là hình vuông số lẻ.

Như vậy, đồ hình Lạc thư ngoài tròn trong vuông đã hình thành.

Đồ hình Lạc thư ngoài tròn trong vuông của Vạn Niên Thuần là thể hiện trong trạng thái tĩnh, giờ chúng ta xem xét đến hiệu quả của đồ hình này trong trạng thái động.

Hình 1: 4 chỉ 2, 2 chỉ 6, 6 chỉ 8, 8 chỉ 4; 9 chỉ 2, 2 chỉ 7, 7 chỉ 6, 6 chỉ 1, 1 chỉ 8, 8 chỉ 3, 3 chỉ 4, 4 chỉ 9. Hình này được gọi là hình toàn cơ theo hướng xuôi:

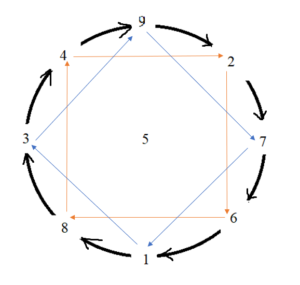
Hình 2: 4 chỉ 8, 8 chỉ 6, 6 chỉ 2, 2 chỉ 4; 9 chỉ 3, 3 chỉ 1, 1 chỉ 7, 7 chỉ 9; 9 chỉ 4, 4 chỉ 3, 3 chỉ 8, 8 chỉ 1, 1 chỉ 6, 6 chỉ 7, 7 chỉ 2, 2 chỉ 9. Hình này được gọi là hình toàn cơ theo hướng ngược:

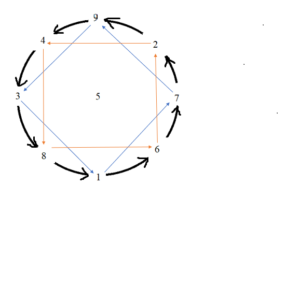
Chúng ta đã tạo xong hình, hiện giờ có thể lấy số làm phép tính. Cách lấy số vẫn là dùng hình toàn cơ hướng xuôi và hình toàn cơ hướng ngược đối ứng mà lấy số.

Một phần tư đường tròn hai đầu là số chẵn.

Lấy theo hướng xuôi: 492, 276, 618, 834.

Lấy theo hướng ngược: 438, 816, 672, 294.

492+276+618+834=2220

438+816+672+294= ?

492^2+276^2+618^2+834^2= 1395720

438^2+816^2+672^2+294^2= ?

492^3+276^3+618^3+834^3=956242800

438^3+816^3+672^3+294^3=?

Có bạn nhắc nhở tôi, rằng cách tính này của anh không sai chứ, nếu viết bừa thì có thể gây ảnh hưởng không tốt, chúng ta cần chú ý chất lượng bài viết. Ha ha, lời nhắc nhở này tốt, các phép tính này, lưu lại một nửa để bạn đọc tự tính. Xin bổ sung chút, ^2 là bình phương, ^3 là lập phương.

Một phần tư đường tròn hai đầu là số lẻ.

Lấy theo hướng xuôi: 927, 761, 183, 349

Lấy theo hướng ngược: 943, 381, 167, 729

927+761+183+349=2220

943+381+167+729=2220

927^2+761^2+183^2+349^2=1593740

943^2+381^2+167^2+729^2=1593740

927^3+761^3+183^3+349^3=1285946100

943^3+381^3+167^3+729^3=1285946100

Toàn bộ hình tròn số chẵn:

Lấy theo hướng xuôi: 49276183, 27618349, 61834927, 83492761

Lấy theo hướng ngược: 43816729, 81672943, 67294381, 29438167

49276183+27618349+61834927+83492761=222222220

43816729+81672943+67294381+29438167=222222220

49276183^2+27618349^2+61834927^2+83492761^2=13985514749033740

43816729^2+81672943^2+67294381^2+29438167^2=13985514749033740

49276183^3+27618349^3+61834927^3+83492761^3=959177030199175157646100

43816729^3+81672943^3+67294381^3+29438167^3=959177030199175157646100

Toàn bộ hình tròn số lẻ:

Lấy theo hướng xuôi: 92761834, 76183492, 18349276, 34927618

Lấy theo hướng ngược: 94381672, 38167294, 16729438, 72943816

92761834+76183492+18349276+34927618=222222220

94381672+38167294+16729438+72943816=222222220

92761834^2+76183492^2+18349276^2+34927618^2=15965316729235720

94381672^2+38167294^2+16729438^2+72943816^2=15965316729235720

92761834^3+76183492^3+18349276^3+34927618^3=1289144023599835190642800

94381672^3+38167294^3+16729438^3+72943816^3=1289144023599835190642800

Ở đây xin chỉ ra một điểm, trên thực tế, toàn bộ tình hình đã được bao hàm trong “Toàn bộ hình tròn số lẻ” và “Toàn bộ hình tròn số chẵn”. Xin chú ý, từ 1 đến 9, chỉ có 9 chữ số, không dùng đến số 5, thì trong quá trình tổ hợp không có các số mà chữ số bị lặp lại, nhiều nhất chỉ có 8 chữ số. Do vậy, hai tình huống này đã đạt tới tình huống cực hạn. Nếu dùng đến 5, thì yêu cầu là trong lúc lấy số theo hướng xuôi và lấy số theo hướng ngược đều phải là 5. Điểm này trong một bài mạn đàm trước đây, nói về hình chữ vạn, đã có ví dụ rồi.

Hình vuông số lẻ:

Lấy theo hướng xuôi: 97, 71, 13, 39

Lấy theo hướng ngược: 93, 31, 17, 79

97+71+13+39=220

93+31+17+79=220

97^2+71^2+13^2+39^2=16140

93^2+31^2+17^2+79^2=16140

97^3+71^3+13^3+39^3=1332100

93^3+31^3+17^3+79^3=1332100

Hình vuông số chẵn:

Lấy theo hướng xuôi: 42, 26, 68, 84

Lấy theo hướng ngược: 48, 86, 62, 24

42+26+68+84=220

48+86+62+24=220

42^2+26^2+68^2+84^2=14120

48^2+86^2+62^2+24^2=14120

42^3+26^3+68^3+84^3=998800

48^3+86^3+62^3+24^3=998800

Cuối cùng, xin để lại cho bạn đọc một chút luyện tập tính toán:

Đường thẳng cộng đoạn cong:

Lấy theo hướng xuôi: 427, 261, 683, 849

Lấy theo hướng ngược: 481, 867, 629, 243

427+261+683+849=

481+867+629+243=

427^2+261^2+683^2+849^2=

481^2+867^2+629^2+243^2=

427^3+261^3+683^3+849^3=

481^3+867^3+629^3+243^3=

Nói chung, hướng xuôi được các số a, b, c, d; hướng ngược được e, f, g, h. Vậy thì được:

Tổng các số：a+b+c+d=e+f+g+h

Tổng bình phương：a^2+b^2+c^2+d^2=e^2+f^2+g^2+h^2

Tổng lập phương：a^3+b^3+c^3+d^3=e^3+f^3+g^3+h^3

Chúng tôi viết nhiều biểu thức như vậy, trên thực tế, các số được lấy có thể đạt đến mức lớn tùy ý, ví dụ lấy việc chạy theo vòng tròn tuần hoàn mà lấy số, thì chọn lấy 8 số có 99999 chữ số cũng rất dễ dàng.

Chỉ có 9 số là hết, mà biểu thức vô cùng.

Có bạn sẽ suy xét, các loại tổng bình phương, lập phương và các hiện tượng phía sau, có nội hàm sâu hơn không? Vấn đề này đã tiếp cận đến bản chất, tôi biết thứ sâu hơn là gì. Ở đây chỉ viết một câu nói đùa, đáp án là có liên quan đến tam tài Thiên Địa Nhân. Nếu có cơ hội tiếp tục viết các bài giải Lạc thư, có thể tôi sẽ nói chi tiết vấn đề này. Nói thật, làm các bài viết về toán thuật có chút gian khổ, cứ phải trình bày phép tính tới lui, xác nhận kết quả chính xác không sai.