Tìm hiểu về Confusion matrix trong Machine Learning?

Trong những bài toán phân loại lớp, sau khi đã xử lý dữ liệu và đưa vào mô hình học máy, đầu ra của mô hình sẽ là một vector xác suất tương ứng của từng lớp. Ta có thể đánh giá mức độ chính xác của mô hình thông qua chỉ số về accuracy (độ chính xác): là phần trăm các lớp đã phân loại đúng / tổng số dự đoán, thế nhưng với chỉ số các lớp đã phân loại sai thì sao. Giả sử với bài toán chuẩn đoán ung thư với việc phân loại một người thành 2 lớp: bị ung thư và không bị ung thư. Nếu trong 100 người cần phân loại có 10 người bị ung thư mà mô hình dự đoán cả 100 người đều không bị ung thư thì độ chính xác của mô hình đã là 0.9 rồi, khá cao phải không. Nhưng với 10 người bị ung thư đã bị bỏ qua thì rõ ràng mô hình này không đáng tin cậy chút nào. Cần phải có một phương pháp đánh giá tốt hơn là độ chính xác trong bài toán phân loại và một trong đó là sử dụng Confusion matrix.

Confusion Matrix là gì?

Là một phương pháp đánh giá kết quả của những bài toán phân loại với việc xem xét cả những chỉ số về độ chính xác và độ bao quát của các dự đoán cho từng lớp. Một confusion matrix gồm 4 chỉ số sau đối với mỗi lớp phân loại:

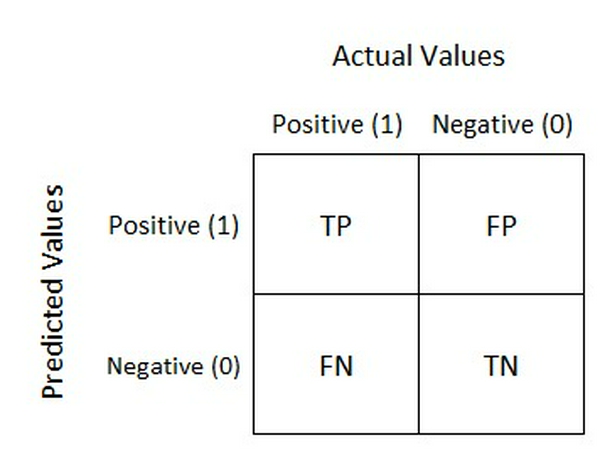
Để đơn giản hóa, ta sẽ sử dụng lại bài toán về chẩn đoán ung thư để giải thích 4 chỉ số này. Trong bài toán chuẩn đoán ung thư ta có 2 lớp: lớp bị ung thư được chuẩn đoán Positive và lớp không bị ung thư được chuẩn đoán là Negative:

• TP (True Positive): Số lượng dự đoán chính xác. Là khi mô hình dự đoán đúng một người bị ung thư.
• TN (True Negative): Số lương dự đoán chính xác một cách gián tiếp. Là khi mô hình dự đoán đúng một người không bị ung thư, tức là việc không chọn trường hợp bị ung thư là chính xác.
• FP (False Positive - Type 1 Error): Số lượng các dự đoán sai lệch. Là khi mô hình dự đoán một người bị ung thư và người đó hoàn toàn khỏe mạnh.
• FN (False Negative - Type 2 Error): Số lượng các dự đoán sai lệch một cách gián tiếp. Là khi mô hình dự đoán một người không bị ung thư nhưng người đó bị ung thư, tức là việc không chọn trường hợp bị ung thư là sai.

Từ 4 chỉ số này, ta có 2 con số để đánh giá mức độ tin cậy của một mô hình:

• Precision: Trong tất cả các dự đoán Positive được đưa ra, bao nhiêu dự đoán là chính xác? Chỉ số này được tính theo công thức

• Recall: Trong tất cả các trường hợp Positive, bao nhiêu trường hợp đã được dự đoán chính xác? Chỉ số này được tính theo công thức:

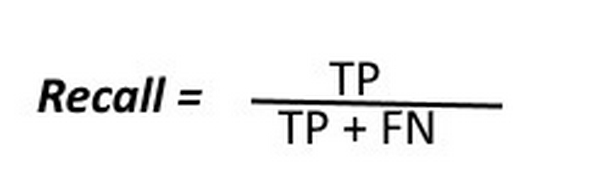
Quay trở lại với bài toán chẩn đoán ung thư, giả sử ta có 1 tập dữ liệu gồm 100 người với 90 người khỏe mạnh(Negative) và 10 người mắc bệnh ung thư(Positive) và mô hình dự đoán đúng 2/10 người bị ung thư, tức là đưa ra dự đoán 2 người bị ung thư thì cả 2 dự đoán đều chính xác. Như vậy, chỉ số về Precision khi dự đoán lớp ung thư là 1. Tuy nhiên, 8/10 người còn lại đã bị bỏ qua, từ đó chỉ số về Recall chỉ là 0.2 - một con số rất thấp. Để đánh giá độ tin cậy chung của mô hình, người ta đã kết hợp 2 chỉ số Precision và Recall thành một chỉ số duy nhất: F-score, được tính theo công thức:

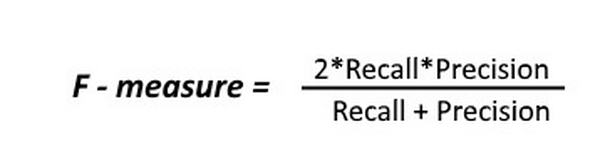
Một mô hình có chỉ số F-score cao chỉ khi cả 2 chỉ số Precision và Recall để cao. Một trong 2 chỉ số này thấp đều sẽ kéo điểm F-score xuống. Trường hợp xấu nhất khi 1 trong hai chỉ số Precison và Recall bằng 0 sẽ kéo điểm F-score về 0. Trường hợp tốt nhất khi cả điểm chỉ số đều đạt giá trị bằng 1, khi đó điểm F-score sẽ là 1.

Qua việc sử dụng chỉ số F-score, ta đã có một thước đo đáng tin cậy về hiệu năng của mô hình trong các bài toán phân loại, đặc biệt khi dữ liệu về một lớp lớn hơn gấp nhiều lần so với dữ liệu về lớp còn lại như trong bài toán chẩn đoán ung thư. Cảm ơn các bạn đã đọc bài viết :D.

Nguồn: towardsdatascience Understanding Confusion Matrix