Tìm hiểu chi tiết về AUC - ROC trong Machine Learning?

Tìm hiểu về AUC - ROC trong Machine Learning

Trong lĩnh vực Machine Learning, việc tính toán hiệu suất của mô hình là một điều rất quan trọng. Trong các bài toán phân loại, ngoài phương pháp phổ biến là sử dụng Confusion Matrix thì còn phải nhắc đến một phương pháp rất quan trọng khác, đó là đường cong AUC - ROC. Bài viết này sẽ giới thiệu về AUC - ROC và các ứng dụng cùa nó.

AUC - ROC là gì?

AUC - ROC là một phương pháp tính toán hiệu suất của một mô hình phân loại theo các ngưỡng phân loại khác nhau. Giả sử với bài toán phân loại nhị phân (2 lớp) sử dụng hồi quy logistic (logistic regression), việc chọn các ngưỡng phân loại [0..1] khác nhau sẽ ảnh hưởng đến khả năng phân loại của mô hình và ta cần tính toán được mức độ ảnh hưởng của các ngưỡng. AUC là từ viết tắt của Area Under The Curve còn ROC viết tắt của Receiver Operating Characteristics. ROC là một đường cong biểu diễn xác suất và AUC biểu diễn mức độ phân loại của mô hình. AUC-ROC còn được biết đến dưới cái tên AUROC (Area Under The Receiver Operating Characteristics). Ý nghĩa của AUROC có thể diễn giải như sau: Là xác suất rằng một mẫu dương tính được lấy ngẫu nhiên sẽ được xếp hạng cao hơn một mẫu âm tính được lấy ngẫu nhiên. Biểu diễn theo công thức, ta có AUC = P(score(x+) > score(x-)). Chỉ số AUC càng cao thì mô hình càng chính xác trong việc phân loại các lớp.

Đường cong ROC biểu diễn các cặp chỉ số (TPR, FPR) tại mỗi ngưỡng với TPR là trục tục và FPR là trục hoành.

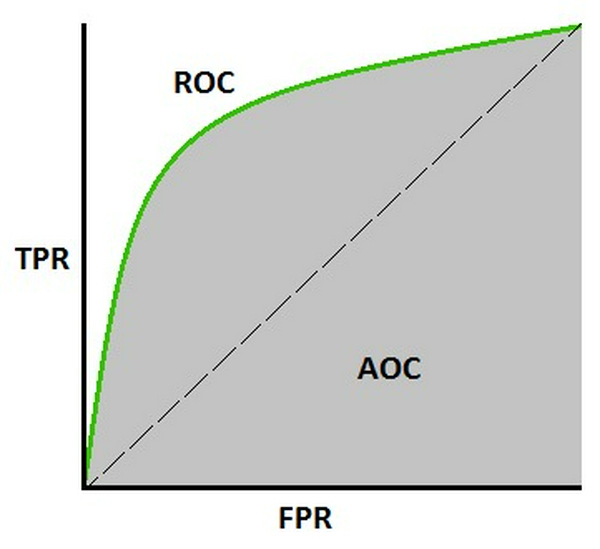
Các chỉ số sử dụng trong AUC - ROC

TPR(True Positive Rate/Sentivity/Recall): Biểu diễn tỷ lệ phân loại chính xác các mẫu dương tính trên tất cả các mẫu dương tính, được tính theo công thức:

TPR càng cao thì các mẫu dương tính càng được phân loại chính xác.

Specificity: Biểu diễn tỷ lệ phân loại chính xác các mẫu âm tính trên tất cả các mâu âm tính, được tính theo công thức:

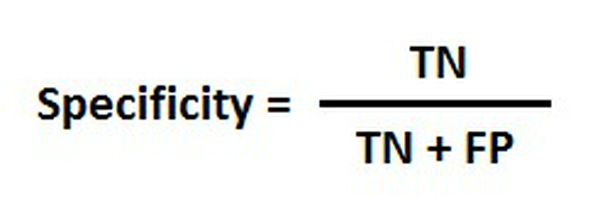
FPR(False Positive Rate/Fall-out): Biểu diễn tỷ lệ gắn nhãn sai các mẫu âm tính thành dương tính trên tất cả các mẫu âm tính, được tính theo công thức:

Có thể thấy Specificity tỷ lệ nghịch với FPR. FPR càng cao thì Specificity càng giảm và số lượng các mẫu âm tính bị gắn nhãn sai càng lớn.

Đây chính là các chỉ số dùng để tính toán hiệu suất phân loại của mô hình. Để hợp chúng lại thành 1 chỉ số duy nhất, ta sử dụng đường cong ROC để hiển thị từng cặp (TPR, FPR) cho các ngưỡng khác nhau với mỗi điểm trên đường cong biểu diễn 1 cặp (TPR, FPR) cho 1 ngưỡng, sau đó tính chỉ số AUC cho đường cong này. Chỉ số AUC chính là con số thể hiện hiệu suất phân loại của mô hình.

Đánh giá mô hình qua chỉ số AUC

Như đã nói ở trên, chỉ số AUC càng gần 1 thì mô hình càng phân loại chính xác. AUC càng gần 0.5 thì hiệu suất phân loại càng tệ còn nếu gần 0 thì mô hình sẽ phân loại ngược kết quả (phân loại dương tính thành âm tính và ngược lại). Giờ ta sẽ biểu diễn các trường hợp này qua các đồ thị.

Ghi chú: Đường cong màu đỏ biểu diễn phân phối của các mẫu dương tính, đường cong màu xanh lá biểu diễn phân phối của các mẫu âm tính:

• AUC = 1

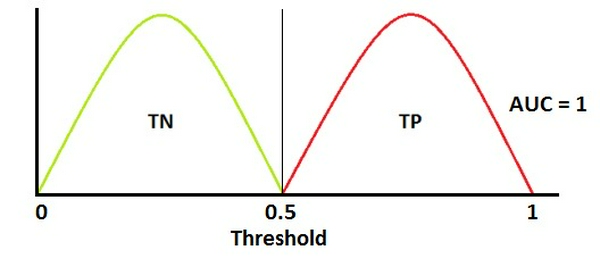
Đây là trường hợp tốt nhất. Mô hình phân loại hoàn toàn chính xác khi 2 đường cong không chồng lên nhau. Tuy nhiên trường hợp này rất khó xảy ra và chỉ tồn tại trên lý thuyết.

• AUC = 0.7

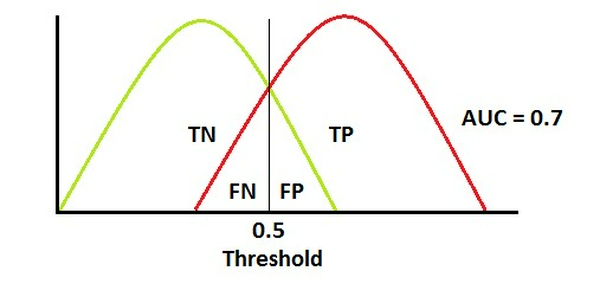
Khi 2 đường cong chồng lên nhau, việc phân loại sẽ xảy ra 2 dạng lỗi đó là FP(Type 1 Error) và FN(Type 2 Error). Ta có thể thay đổi giá trị của 2 chỉ số lỗi này bằng cách thay đổi ngưỡng. Có thể thấy đường cong ROC đã hạ xuống một chút, tuy nhiên nó vẫn nằm ở góc trên bên trái của đồ thị, tức là hiệu suất phân loại vẫn ổn định.

• AUC = 0.5

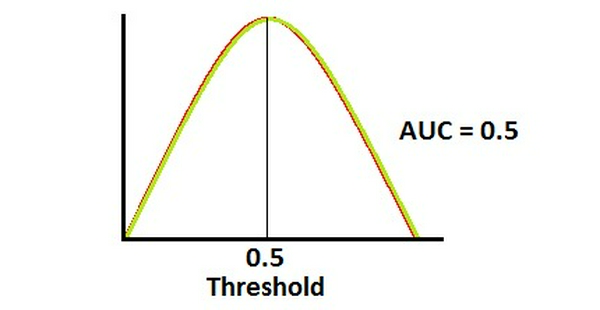
Đây là trường hợp tệ nhất. Mô hình hoàn toàn không có khả năng phân loại giữa 2 lớp.

Đường cong ROC ở trường hợp này là một đường thẳng tạo với Ox một góc 45 độ, biểu diễn một mô hình phân loại một cách ngẫu nhiên. Mô hình phân loại ngẫu nhiên thường được sử dụng như một đường cơ sở để so sánh giữa các mô hình.

• AUC = 0

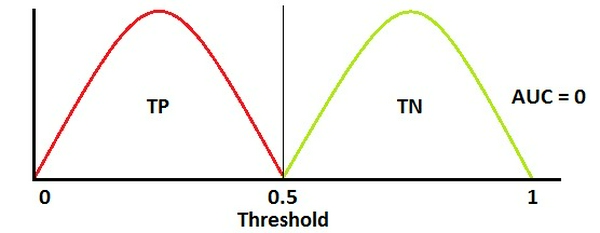
Khi AUC xâp xỉ 0, mô hình phân loại ngược hoàn toàn 2 lớp với việc phân loại âm tính thành dương tính - dương tính thành âm tính. Để sửa điều này ta chỉ cần đảo ngược đầu ra của mô hình.

Mối liên hệ giữa Specificity - Sentivity, TPR - FPR

• Sentivity và Specificity là 2 chỉ số tỷ lệ nghịch với nhau. Khi chỉ số Sentivity tăng thì chỉ số Specificity giảm và ngược lại.
• Khi ta tăng ngưỡng phân loại, số lượng mẫu được gắn nhãn âm tính sẽ tăng lên, từ đó chỉ số Specificity tăng và chỉ số Sentivity giảm. Điều ngược lại cũng đúng.
• Vì Sentivity/TFP và FPR đều tỉ lệ nghịch với Specificity nên TFP tỷ lệ thuận với FPR.

Sử dụng AUC - ROC cho bài toán phân loại đa lớp

Khi số lớp cần phân loại lớn hơn 2, ta có thể áp dụng phương thức One vs All như sau: cho 3 lớp cần phân loại X, Y, Z. Đầu tiên ta sẽ phân loại 2 lớp: X và (Y hoặc Z) và tính toán AUC cho phân loại này. Sau đó tiếp tục với phân loại 2 lớp: Y và (X hoặc Z) và cuối cùng là 2 lớp: Z và (X hoặc Y).

Cảm ơn các bạn đã đọc bài viết :D.

Nguồn: TowardsDataScience Understanding AUC - ROC