Nghịch lý zenon - Achilles và con rùa?

Trong 1 cái group mềnh tham gia có 1 bạn hỏi cách phản biện lại nghịch lý zenon bằng lập luận toán học với kiến thức toán cấp 3 (vì bạn kia đang học cấp 3). Lâu quá rồi nên mềnh cũng ko nhớ được là toán cấp 3 học đến đâu rồi nữa, bạn nào có ý tưởng gì về cái này ko?

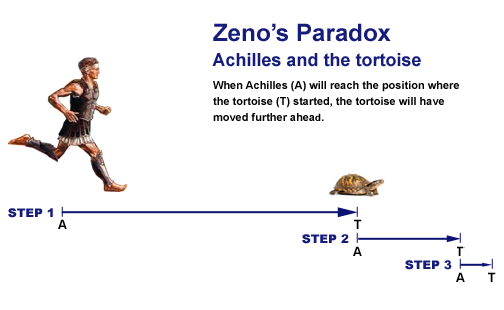
Nghịch lý zenon: "Trong một cuộc chạy đua, người chạy nhanh nhất không bao giờ có thể bắt kịp được kẻ chậm nhất. Kể từ khi xuất phát, người đuổi theo trước hết phải đến được điểm mà kẻ bị đuổi bắt đầu chạy. Do đó, kẻ chạy chậm hơn luôn dẫn đầu"

Có vẻ cái mệnh đề kia hơi rắc rối khó hiểu, ví dụ này có vẻ sẽ dễ hình dung hơn:

Achilles chạy đua với rùa. Ví dụ Achilles chấp rùa một đoạn 100 mét. Nếu chúng ta giả sử rằng mỗi tay đua đều bắt đầu chạy với một tốc độ không đổi (Achilles chạy rất nhanh và rùa rất chậm), thì sau một thời gian hữu hạn, Achilles sẽ chạy được 100 mét, tức anh ta đã đến được điểm xuất phát của con rùa. Nhưng trong thời gian này, con rùa cũng đã chạy được một quãng đường ngắn, ví dụ 10 mét. Sau đó Achilles lại tốn một khoảng thời gian nữa để chạy đến điểm cách 10 mét ấy, mà trong thời gian đó thì con rùa lại tiến xa hơn một chút nữa, và cứ như thế mãi. Vì vậy, bất cứ khi nào Achilles đến một vị trí mà con rùa đã đến, thì con rùa lại cách đó một đoạn.