Gradient Descent: Giải pháp tối ưu hóa bài toán Machine Learning
Ở bài viết này tôi sẽ giới thiệu trực quan về Gradient Descent.
Trước tiên, chúng ta hãy cùng tìm hiểu Gradient Descent là gì?
- Nó là một thuật toán tối ưu hóa được sử dụng để tìm ra các giá trị của tham số, hệ số của hàm (f), giảm thiểu hàm chi phí (cost).
- Nó còn được định nghĩa là một thuật toán tối ưu hóa số lần lặp (thứ tự lặp) để tìm ra min của hàm loss function.
- Nó thực hiện các bước tỷ lệ nghịch với gradient của hàm tại thời điểm hiện tại.

- Nó cũng làm một trong những thuật toán dùng để tối ưu hóa sử dụng rộng rãi nhất.
Cho một model machine learning với tham số (weights và biases) và một hàm chi phí để xem mô hình tốt như thế nào, vấn đề là làm thế nào để giảm chi phí để tìm ra một tập weights phù hợp nhất với chi phí ít nhất.

Gradient descent là một phép lặp. Chính vì vậy mà tôi sẽ bắt đầu với một số giá trị cho các thông số của model (weights và biases), tôi sẽ cải thiện chúng từ từ.
Để cải thiện weights, chúng ta cần phải tính toán hàm chi phí cho weights tương ứng với weights hiện tại và di chuyển chúng theo hướng mà hàm cost function giảm dần (giảm hoặc âm) - tính toán độ dốc. Vì vậy mà quá trình này phải lặp đi lặp lại hàng trăm (hàng ngàn) lần để tìm ra giải pháp.
Gradient descent được sử dụng để làm giảm thiểu một hàm cost function J(w) tham số ở đây là w. Đạo hàm sẽ cho chúng ta thấy được độ dốc và xiên của hàm cost function. Vì vậy mà để tối giản hóa cost function, chúng ta cần di chuyển ngược lại hướng của đạo hàm.
Gọi G là gradient (đạo hàm) của hàm chi phí đối với các tham số tại một giá trị cụ thể (w) của vector trọng số, ta được:
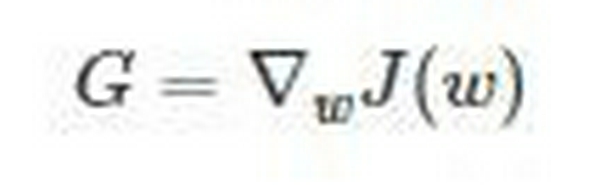
Sau đó, độ dốc của đạo hàm được đưa ra bởi công thực:
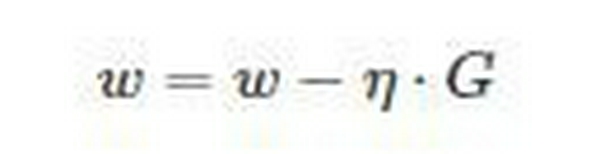
η =
Các bước thực hiện:
- Khởi tạo giá trị w ngẫu nhiên
- Tính đạo hàm gradient G của các thông số w.r.t
- Cập nhật weights: w = w -ηG
- Lặp lại cho đến khi J(w) ngừng giảm hoặc các điều kiện dừng khác xảy ra.
Hãy tưởng tượng bà hiểu rõ hơn vấn đề bằng ví dụ dưới đây:
Hãy tưởng tượng bạn bị mù, và cần phải lái xe ô tô đi qua một đoạn đường gấp khúc (như hình dưới đây), và mục tiêu của bạn là vượt qua độ cao thấp nhất. Một trong những chiến lược theo đơn giản nhất là bạn di chuyển bánh xe lên xuống theo độ dốc của đoạn đường, và cần xem xét rằng nó có đang di chuyển theo một đường mà mặt đất đang xuống dốc nhanh nhất (bánh xe di chuyển nhanh hơn theo hướng đó). Nếu bạn cứ lặp lại quá trình đó (lên dốc rồi lại lùi về xuống dốc, chỉ lặp ở một đoạn như hình dưới đây) thì đến một thời điểm nào đó, vị trí mà xe dừng lại chính là vị trí thấp nhất của đoạn đường.

Chiếc xe kia tương tự như hàm cost function.
Làm giảm cost function tương tự như khi cố gắng đạt đến vị trí thấp hơn.
Cảm nhận được chính xác chiếc xe có đang đi xuống hay không (xuống dốc) chính là tính toán độ dốc và thực hiện lặp nhiều lần việc di chuyển xe chính là lặp cho tham số.
Dưới đây là một số loại gradient descent. Tùy thuộc vào dữ liệu đang được sử dụng mà dùng một loại gradient descent khác. Lý do cho sự phân loại này là hiệu quả tính toán của các mô hình vì chúng có nhiều điểm dữ liệu trên một tập dữ liệu và nó được chia thành các loại: Batch gradient descent, Stochastic gradient descent & Mini-Batch Gradient descent.
Cảm ơn các bạn vì đã theo dõi!
Hi vọng bài viết sẽ giúp ích cho các bạn
