Giới thiệu về tư duy Bayesian: Từ định lý Bayes đến Mạng Bayes

Giả sử rằng thế giới xuất hiện một căn bệnh rất hiếm gặp với tỷ lệ người mắc bệnh chỉ là 1/1000. Bạn muốn kiểm tra xem mình có bị bệnh hay không nên đã tạo một bộ kiểm tra có 99% độ chính xác. Khi sử dụng bộ kiểm tra lên chính mính, kết quả trả về là dương tính. Liệu bạn có thật sự đen đủi đến vậy hay bộ test đã rơi vào 1% sai sót ? Để cho chắc, bạn tiếp tục kiểm tra lại mình một lần nữa với hy vọng bộ test đã sai sót trong lần thử đầu tiên. Vậy kết quả của lần thử thứ 2 sẽ thay đổi niềm tin về tỷ lệ mắc bệnh của bạn như thế nào? Sử dụng định lý Bayes và mạng Bayes, chúng ta sẽ mô phỏng lại bài toán trên.

Lần thử đầu tiên

Ta có bảng xác suất điều kiện (Conditional Probability Table) của căn bệnh hiếm gặp này như sau:

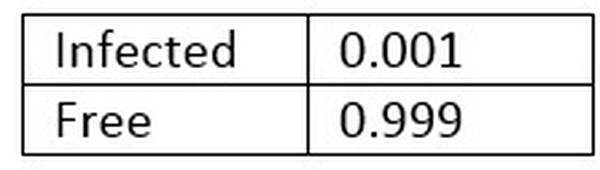
Ta có thể thấy rằng, tỷ lệ mắc bệnh chỉ là 1/1000 = 0.001, đồng nghĩa với việc tỷ lệ không mắc bệnh là 999/1000 = 0.999. Bảng tiếp theo biểu diễn độ chính xác của bộ kiểm tra bạn đã xây dựng:

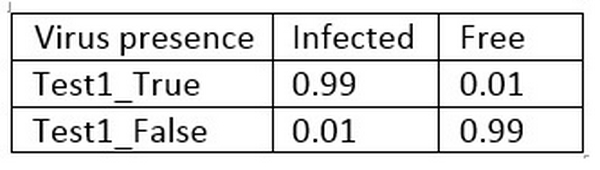
Vì bộ kiểm tra có 99% độ chính xác, nếu bạn mắc bệnh thì bộ kiểm tra sẽ trả về dương tính với 99% (1% trả về âm tính) còn nếu bạn không mắc bệnh thì bộ kiểm tra sẽ trả về âm tính với 99% (1% trả về dương tính). Ở cả 2 trường hợp tỷ lệ sai sót chỉ là 1%.

Dưới đây là một mạng Bayesian đơn giản biểu diễn sự phụ thuộc của kết quả test với việc bạn có mắc bệnh hay không:

Giả sử rằng kết quả test trả về là dương tính(True), vậy xác suất bạn mắc bệnh là bao nhiêu? Chúng ta có thể tính được xác suất này sử dụng định lý Bayes:

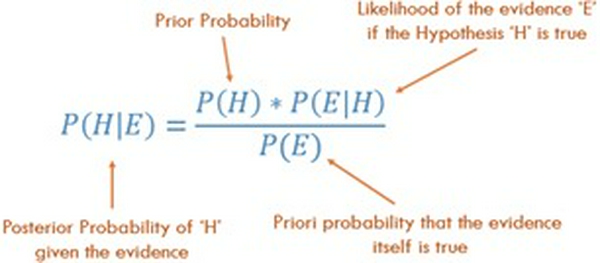
Trong đó:

• H là sự kiện bạn mắc bệnh
• E là sự kiện bộ test trả về dương tính

Gọi:

• Hc là sự kiện bạn không mắc bệnh
• Ec là sự kiện bộ test trả về âm tính

Từ công thức trên, ta cần tính 𝑃(H|E):

𝑃(H|E) = 𝑃(H) × 𝑃(E|H) / 𝑃(E)

𝑃(H|E) = 𝑃(H) × P(E|H) / ( 𝑃(E|H) × 𝑃(H) + 𝑃(E|Hc) × 𝑃(Ec) )

𝑃(H|E) = 0,001*0,99 / (0,99*0.001 + 0,01*0,999) = 0,9 = 9%

Vậy, ngay cả khi bộ test có độ chính xác 99% trả về dương tính, xác suất bạn bị mắc bệnh chỉ là 9%.

Lần thử thứ 2

Kết quả sẽ thay đổi ra sao nếu ta kiểm tra lại một lần nữa? Sử dụng lại định lý Bayes, ta có thể tính được xác suất mắc bệnh theo 2 trường hợp:

• Bộ test thứ 2 trả về dương tính: Tính toán tương tự, ta có mạng Bayesian với 2 bộ test trả về dương tính như sau

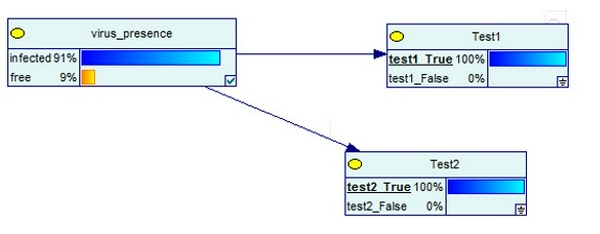
Điều này có nghĩa là, với 2 kết quả kiểm tra là dương tính, xác suất mắc bệnh của bạn đã tăng từ 9% lên tới 91%. Điều này hoàn toàn hợp lý vì ngay cả khi tỷ lệ mắc bệnh rất thấp nhưng với 2 lần kiểm tra với độ chính xác gần như hoàn hảo (99%) thì xác suất mắc bệnh tăng lên rất nhanh.

• Bộ test thứ 2 trả về âm tính: Tỷ lệ mắc bệnh giảm còn 0%.

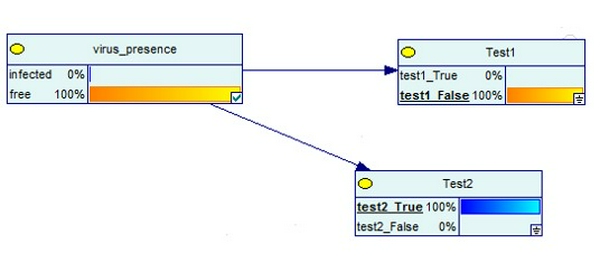
Với 3 lần thử

Nếu thực hiển 3 lần kiểm tra tương tự với độ chính xác giống nhau, ta có các trường hợp:

• 3 kết quả đều dương tính: Chia buồn với bạn, xác suất mắc bệnh đã tăng thành 100%.

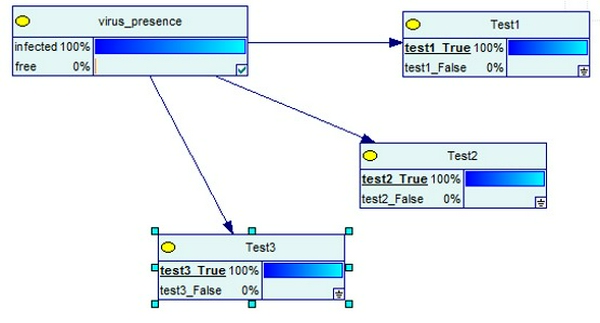
• 2 kết quả dương tính và 1 âm tính: Xác suất mắc bệnh lại quay về 91%

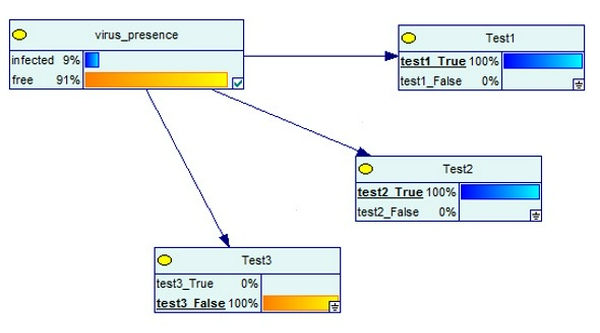
Kết luận

Mạng Bayesian là một công cụ hữu hiệu để biểu diễn lối tư duy Bayesian và được sử dụng rộng rãi trong ngành khoa học dữ liệu khi khối lượng dữ liệu có kích thước lớn và có tính ngẫu nhiên. Mạng Bayesian cho phép chúng ta mô hình hóa lại những kịch bản khác nhau, biểu diễn độ phụ thuộc xác suất giữa các đầu vào và đầu ra tương ứng.

Bài viết này đã giới thiệu về cách xây dựng một mạng Bayesian đơn giản bắt đầu từ định lý Bayes. Cảm ơn các bạn đã đọc và hẹn gặp lại :D.

Nguồn: TowardsDatascience Introduction to Bayesian Thinking: from Bayes theorem to Bayes networks