Giới thiệu về Naive Bayes trong Machine Learning

Naive Bayes là một mô hình học giám sát dựa trên xác suất rất phổ biến trong Machine Learning. Để có một cái nhìn tổng quan về mô hình này, chúng ta hãy cùng đi qua một ví dụ đơn giản sau đây:

Bạn có 2 người bạn là Trang và Huy. Mỗi người có một cách nói chuyện khác nhau và thói quen sử dụng từ ngữ khác nhau. Giả sử rằng Trang rất hay sử dụng 3 từ ngữ [yêu, đẹp, tuyệt] còn Huy hay sử dụng 3 từ [cún, bóng, tuyệt]. Rồi một ngày, bạn nhận được một tin nhắn từ một số máy lạ nhưng những người biết số bạn chỉ có thể là Trang hoặc Huy. Tin nhắn có nội dung: “Tớ yêu bãi biển Nha Trang. Hoàng hôn trên bãi biển có khung cảnh thật đẹp!”. Liệu bạn có thể đoán được ai là người gửi không?

Nếu bạn đoán người gửi là Trang thì chắc hẳn bạn đã đúng. Có lẽ bởi vì trong nội dung có 2 từ yêu và đẹp hay được Trang sử dụng, từ đó bạn có thể suy luận rằng xác suất người gừi là Trang sẽ cao hơn. Giờ chúng ta sẽ bắt đầu đi sâu hơn một chút bằng cách áp dụng các xác suất vào trong ví dụ. Giả sử rằng bạn biết xác suất Trang gửi tin nhắn cho bạn là 0.4, xác suất Huy gửi tin nhắn cho bạn là 0.6 và 2 người sử dụng các từ ngữ trên với những xác suất như bảng dưới đây:

Trang (0.4)               Huy(0.6)

Yêu: 0.2                     Yêu: 0.05

Đẹp: 0.2                  Đẹp: 0.2

Cún: 0.1                     Cún: 0.25

Bóng: 0.05                Bóng: 0.4

Tuyệt: 0.45               Tuyệt: 0.1

Với tin nhắn có nội dung: "Yêu cún!" thì bạn hãy thử đoán xem ai là người gửi. Để xử lý những bài toán như thế này ta sẽ sử dụng định lý Bayes.

Định lý Bayes

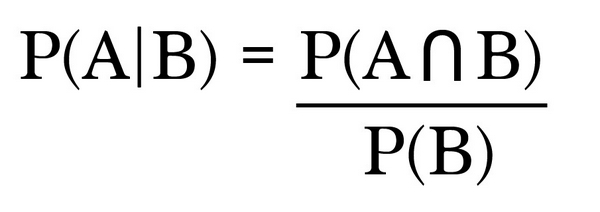
Định lý Bayes được sử dụng để tính toán xác suất sự kiện A xảy ra khi biết sự kiện B đã xảy ra và được ký hiệu là P(A | B), trong đó P(A) là xác suất sư kiện A xảy ra và P(B) là xác suất sự kiện B xảy ra. Giờ ta sẽ áp dụng định lý Bayes để giải quyết bài toán trên. Ta viết lại bảng xác suất theo các ký hiệu đã giới thiệu ở trên như sau:

P(Trang) : 0.4              P(Huy): 0.6

P(Yêu | Trang): 0.2               P(Yêu | Huy): 0.05

P(Đẹp | Trang): 0.2                 P(Đẹp | Huy): 0.2

P(Cún | Trang): 0.1                  P(Cún | Huy): 0.25

P(Bóng | Trang): 0.05            P(Bóng | Huy): 0.4

P(Tuyệt | Trang): 0.45           P(Tuyệt | Huy): 0.1

Với tin nhắn có nội dung: "Yêu cún" ta cùng tính xác suất người gửi là Trang. Áp dụng định lý Bayes ta có:

P(Trang | Yêu cún) = P(Trang) * P (Yêu cún | Trang) / P(Yêu cún)

• Tính P(Yêu cún | Trang): Ta có

P(Yêu cún | Trang) = P(Yêu | Trang) * P(Cún | Trang) = 0.2 (1)

• Tính P(Yêu cún): Áp dụng định lý tổng xác suất, ta có

P(Yêu cún) = P(Yêu cún | Trang) + P(Yêu cún | Huy)

= P(Yêu | Trang) * P(Cún | Trang) + P(Yêu | Huy) * P(Cún | Huy)

= 0.2 + 0.0125 = 0.2125 (2)

Từ (1) và (2), ta có:

P(Trang | Yêu cún) = P(Trang) * P (Yêu cún | Trang) / P(Yêu cún)

 = 0.4 * 0.2 / 0.2125 ~ 0.3765

Các bạn có thể tính xác suất P(Huy | Yêu cún) tương tự như trên rồi từ đó đưa ra kết luận về người gửi. Các tính toán ta vừa thực hiện ở trên chính là một mô hình phân loại Naive Bayes đơn giản.

Mô hình phân loại Naive Bayes

Mô hình Naive Bayes hoạt động bằng cách kết hợp các xác suất của mỗi đầu vào: P(Trang), P(Cún | Trang), ... để tính xác suất của từng lớp với đầu vào đó: P(Trang | Yêu cún), P(Huy | Yêu cún), sau đó chọn lớp có xác suất cao nhất. Một cách tổng quát, với đầu vào E và các lớp X₁, X₂, ..., X_n, ta có quá trình phân loại:

Prediction = max_i ( P(X_i | E) ) , i = [1, n]

với P(X_i | E) được tính theo định lý Bayes như ví dụ trên.

Mô hình phân loại này đặt giả định rằng mỗi thuộc tính của đầu vào ( trong ví dụ trên là mỗi từ ) đều không phụ thuộc với nhau. Tuy nhiên điều này không phải lúc nào cũng đúng, vì vậy mà tên gọi của nó xuất hiện từ Naive (ngây thơ). Như trong ví dụ trên, giữa các từ với nhau đều có mối liên hệ về thứ tự xuất hiện để câu tạo thành có ngữ nghĩa. Dù vậy, Naive Bayes vẫn được sử dụng nhiều vì tính đơn giản trong tính toán và tốc độ huấn luyện và xử lý nhanh. Naive Bayes thường được sử dụng cho các bài toán:

• Dự đoán trong thời gian thực (Real time Prediction)
• Phân loại văn bản (Text classification)
• Lọc thư rác (Spam Filtering)
• Hệ gợi ý (Recommendation System)

Hy vọng rằng qua bài viết này, các bạn đã có một cái nhìn rõ hơn về mô hình phân loại Naive Bayes. Cảm ơn các bạn đã đọc bài viết :D.

Nguồn: Medium Supervised Learning and Naive Bayes Classification