Giới thiệu về mạng Bayesian

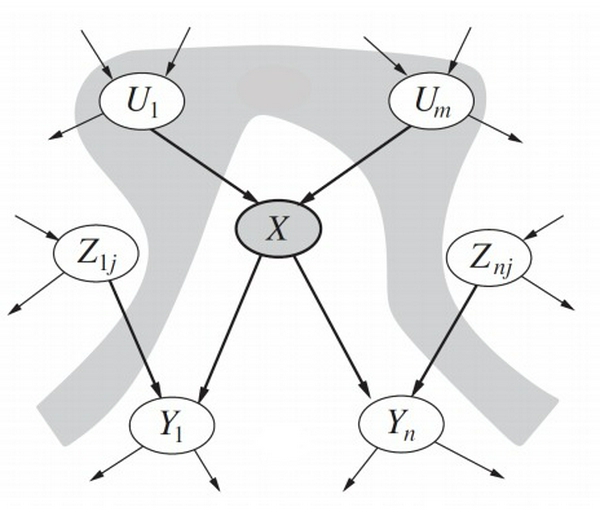
1. Mạng Bayesian là một mô hình xác suất đồ thị sử dụng suy diễn Bayesian để tính toán xác suất. Mục đích của mạng Bayesian là mô hình hóa các phụ thuộc có điều kiện của các biến ngẫu nhiên bằng cách biểu diễn các phụ thuộc đó dưới dạng các cạnh của đồ thị. Đồ thị của mạng Bayesian biểu diễn các mối quan hệ về xác suất và ta có thể sử dụng các quan hệ này để suy diễn và tính toán các biến ngẫu nhiên của đồ thị một cách hiệu quả.

Lý thuyết xác suất

Nhắc lại kiến thức về xác suất một chút, ta biết một phân phối xác suất chung của một tập các biến ngẫu nhiên A₁, A₂, ..., A_n, ký hiệu là P(A₁, A₂, ..., A_n) được tính bằng công thức:

• P(A₁, A₂, ..., A_n) = P(A₁ | A₂, ..., A_n) * P(A₂ | A₃, ..., A_n) * ... * P(A_n)

theo quy tắc chuỗi trong xác suất. Tiếp theo, ta có: Mối quan hệ độc lập có điều kiện (conditional independence) giữa 2 biến ngẫu nhiên A và B khi có một biến ngẫu nhiên thứ 3 là C, được biểu diễn bằng công thức:

• P(A, B | C) = P(A | C) * P(B | C)

Ta nói, 2 biến ngẫu nhiên A và B độc lập với nhau với điều kiện biến C xảy ra. Khi ta biết biến C xảy ra, những thông tin về khi nào biến A xảy ra không cung cấp bất kỳ thông tin gì về biến B và ngược lại. Một công thức khác để biểu diễn quan hệ độc lập có điều kiện như sau:

• P(A | B, C) = P(A | C)

Mạng Bayesian

Sử dụng các mối quan hệ xác suất trong mạng Bayesian, ta có thể biểu diễn các phân phối xác suất chung giữa các biến ngẫu nhiên một các trực quan qua việc sử dụng các mối quan hệ độc lập có điều kiện. Dứới đây là một ví dụ của mạng Bayesian:

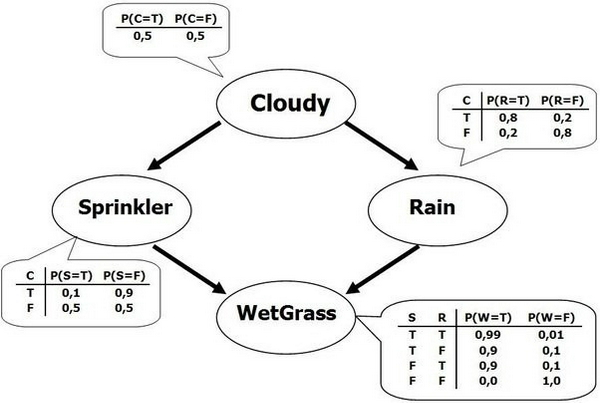
Một mạng Bayesian là một đồ thị có chu kỳ với mỗi nút của mạng biểu diễn một biến ngẫu nhiên và mỗi cạnh biểu diễn mối quan hệ phụ thuộc giữa các biến. Một cạnh (A, B) trong đồ thị biểu diễn xác suất P(B | A) và xác suất này là một hệ số trong phân phối xác suất chung của các biến.

Mạng Bayesian thỏa mãn tính chất cục bộ của Markov (local Markov): Một nút trong đồ thị là độc lập có điều kiện với các nút không phải con của nút đó khi biết nút cha. Ở mạng trên, ta có P(Sprinkler | Cloudy, Rain) = P(Sprinkler | Cloudy) vì biến ngẫu nhiên Sprinkler độc lập có điều kiện với biến ngẫu nhiên Rain - là nút không phải nút con của Sprinkler khi có Cloudy. Tính chất này khiến việc tính toán phân phối xác suất chung trở nên đơn giản hơn rất nhiều. Sau khi đơn giản hóa, phân phối xác suất chung được tính là tích của các phân phối P(X | Cha(X)) như sau:

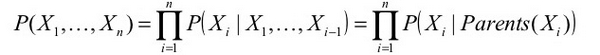
với X_i là một biến ngẫu nhiên trong đồ thị. Với những mạng có kích thước lớn, tính chất này sẽ giảm thiểu chi phí tính toán đi rất nhiều.

Suy diễn Bayesian

Suy diễn trên một mạng Bayesian có thể thực hiện theo 2 dạng:

• Tính toán xác suất chung cho một mảng của đồ thị. Dựa theo công thức trên ta có thể tính toán xác suất này một cách dễ dàng dựa vào các xác suất có điều kiện. Nếu chỉ quan tâm tới một vài biến ngẫu nhiên nhất định, ta cần loại bỏ những biến không quan tâm đến.
• Tìm xác suất P(X | E). xác suất xảy ra của (các) biến ngẫu nhiên X khi (các) biến ngẫu nhiên E xảy ra. Với mạng Bayesian như trên, ta có thể suy diễn xác suất P(Sprinkler, WetGrass | Cloudy) với {Sprinkler, WetGrass} là X còn {Cloudy} là E. Để tính xác suất này, ta sử dụng tính chất P(X | E) = P(X, E) / P(E) = αP(X, E) với α là một hằng số chuẩn hóa. Để tính xác suất P(X | E), ta phải tính xác suất chung trên các biến ngẫu nhiên không xuất hiện ở X và E. Ta ký hiệu tập biến ngẫu nhiên đó là Y.

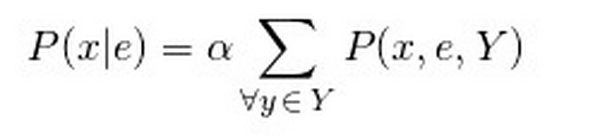
Để tính xác xuất P(Sprinkler, WetGrass | Cloudy), ta áp dụng công thức:

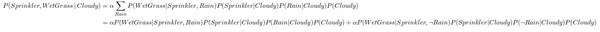
Lưu ý rằng nếu mạng Bayesian có kích thước lớn, tập Y sẽ có nhiều biến ngẫu nhiên vì việc suy diễn xác suất thường chỉ trên một tập nhỏ các biến. Ở những trường hợp này, việc tính toán xác suất sẽ tốn khá nhiều tài nguyên, vì vậy cần có những phương thức tính toán hiệu quả hơn. Các phương pháp có thể sử dụng có thể kể đến như: Variable elimination, Markov chain Monte Carlo,... hoạt động bằng cách ước lượng các xác suất thay vì tính trực tiếp, từ đó giảm bớt quá trình tính toán.

Nguồn: TowardsDataScience Introduction to Bayesian Networks