Deep Learning: Phương pháp kết hợp các hàm Loss và Activation

Mục đích của bài viết này là để hướng dẫn việc sử dụng kết hợp các hàm Loss và Activation phụ thuộc vào mục tiêu của bài toán.

Bài toán Regression: Dự đoán một số thực

Trong bài toán này, layer cuối cùng của mạng neural sẽ chứa một neuron và giá trị đầu ra của nó là một số thực. Giá trị này sẽ sẽ được so sánh với giá trị nhãn để tính độ chính xác của mô hình.

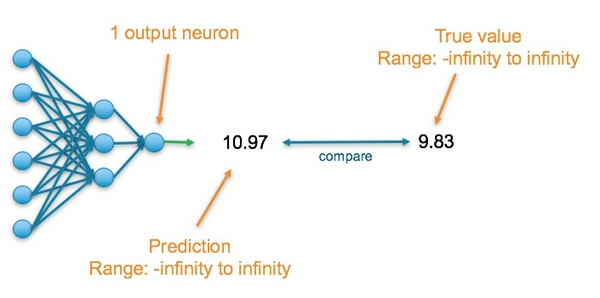
Hàm activation tại layer cuối cùng sẽ là hàm linear:

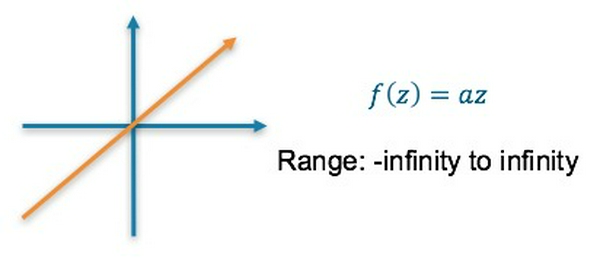
Hàm mất mát: Mean Squared Error (MSE) tính toán giá trị loss bằng cách tìm giá trị trung bình của bình phương giá trị chênh lệch giữa giá trị dự đoán và giá trị thực

Bài toán Classification: Dự đoán 1 lớp trong bài toán phân loại 2 lớp

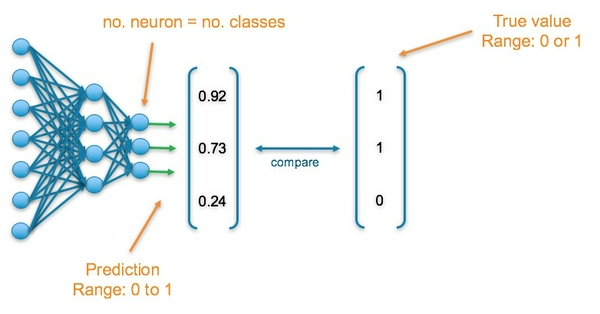
Layer cuối cùng của mạng neural sẽ chứa một neuron và giá trị đầu ra của nó là một số thực nằm trong khoảng [0, 1] biểu diễn xác suất.

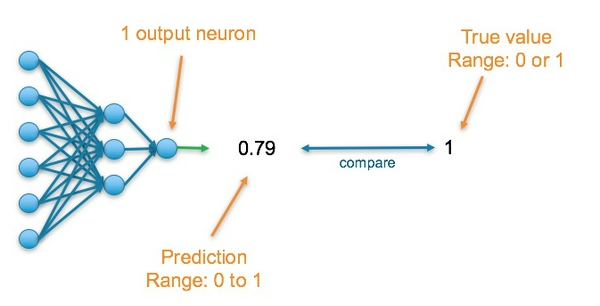
Hàm activation tại layer cuối cùng là hàm sigmoid: Trả về một giá trị nằm trong khoảng [0, 1] biểu diễn xác suất của một lớp.

Hàm mất mát: Binary Cross Entropy tính toán độ chênh lệch giữa 2 phân phối xác suất của dự đoán và của nhãn. Đầu ra của mô hình là phân phối xác suất (p, 1 - p) biểu diễn xác suất xảy ra của một trong hai nhãn. Phân phối xác suất của nhãn có dạng (y, 1 - y) với y nhận giá trị 0 hoặc 1.

Bài toán Classification: Dự đoán 1 lớp trong bài toán phân loại đa lớp

Layer cuối cùng của mạng neural sẽ gồm nhiều neuron với mỗi neuron biểu diễn 1 lớp. Mỗi neuron sẽ nhận giá trị trong khoảng [0, 1] và tổng giá trị các neuron là 1. Vì vậy, đầu ra của mạng neural sẽ là một phân phối xác suất của các lớp

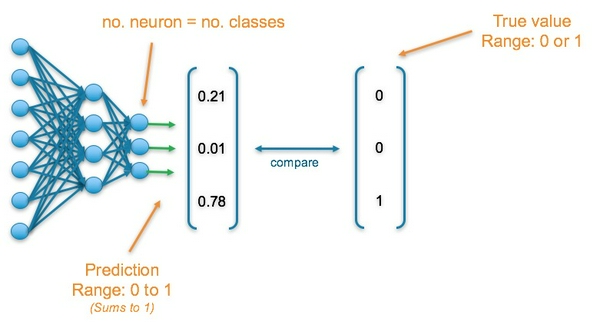
Hàm activation tại layer cuối cùng là hàm softmax: nhận đầu vào là một mảng số thực và đầu ra là một phân phối xác suât với mỗi phần tử nằm trong khoảng [0, 1] và tổng các phần tử là 1

Hàm mất mát: Cross Entropy tính toán độ chênh lệch giữa 2 phân phối xác suất của dự đoán và của nhãn. Nhãn được biến đổi thành một vector one-hot với tất cả phần tử trong vector nhận giá trị 0 trừ một vị trí biểu diễn nhãn nhận giá trị 1. Đầu ra của mô hình là một phân phối xác suất (p1, p2, ..., pn) với n là số lượng các lớp. Phân phối xác suất của nhãn là 1 vector one-hot (0, 0, ... , 1, 0, ..., 0) với vị trí thứ i nhận giá trị 1 tương ứng lớp thứ i.

Bài toán Classification: Dự đoán đa lớp trong bài toán phân loại đa lớp

Layer cuối cùng của mạng neural sẽ gồm nhiều neuron với mỗi neuron biểu diễn 1 lớp. Mỗi neuron sẽ nhận giá trị trong khoảng [0, 1]. Các nhãn sẽ được biểu diễn bằng 1 vector với những vị trí tương ứng với nhãn nhận giá trị 1 và các vị trí còn lại nhận giá trị 0.

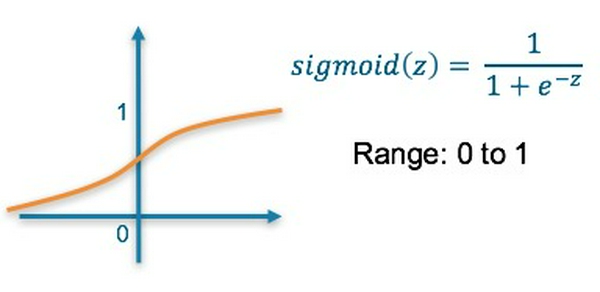
Hàm activation tại layer cuối cùng là hàm sigmoid

Hàm mất mát: Binary Cross Entropy tính toán độ chênh lệch giữa 2 phân phối xác suất của dự đoán và của từng lớp. Mô hình dự đoán một phân phối xác suất (p, 1 - p) đối với từng lớp và so sánh với phân phối thực (y, 1 - y) của từng lớp.

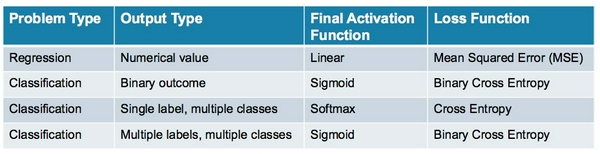
Bảng tổng kết

Cảm ơn các bạn đã đọc bài viết :D

Nguồn: Medium Deep Learning: Which Loss and Activation Functions should I use